VirtualRetina-like Simulator

The Retina model combines filters from convis.filters.retina into a complete model, similar to VirtualRetina [Wohrer2009]. To load the same xml configuration as VirtualRetina, the module convis.retina_virtualretina provides a RetinaConfiguration object and a default configuration.

General Overview

The layers that create the model are:

The formulas on which the classes are based are:

OPL transforms the input with set of linear filters to a center signal \(C\) and a surround signal \(S\) which is subtracted to get the output current \(I_{OLP}\): $$C(x,y,t) = G * T(wu,Tu) * E(n,t) * L (x,y,t)$$ $$S(x,y,t) = G * E * C(x,y,t)$$ $$I_{OLP}(x,y,t) = \lambda_{OPL}(C(x,y,t) - w_{OPL} S(x,y,t)_)$$ \(L\) is the luminance input, \(G\) are spatial (different) filters, \(T\) and \(E\) are temporal filters, \(\lambda_{OPL}\) and \(w_{OPL}\) are scalar weights. Subscripts of the filters are omitted (\(G\) instead of \(G_C\)), but they should be thought of as each being a specific, unique filter.

Here \(*\) is a convolution operator.

Bipolar implements contrast gain control with a differential equation: $$\frac{dV_{Bip}}{dt} (x,y,t) = I_{OLP}(x,y,t) - g_{A}(x,y,t)dV_{Bip}(x,y,t)$$

  • with \(g_{A}(x,y,t) = G * E * Q(V{Bip})(x,y,t)\)
  • and \(Q(V{Bip}) = g_{A}^{0} + \lambda_{A}V^2_{Bip}\)
  • \(G\) and \(E\) are again filters

GanglionInput applies a static nonlinearity and another spatial linear filter: $$I_{Gang}(x,y,t) = G * N(T * V_{Bip})$$

  • with \(N(V) = \frac{i^0_G}{1-\lambda(V-v^0_G)/i^0_G}\) if \(V < v^0_G\)
  • and \(N(V) = i^0_G + \lambda(V-v^0_G)\) if \(V > v^0_G\)

And finally a spiking mechanism GanglionSpiking is implemented by another differential equation:

$$ \dfrac{ dV(x,y) }{dt} = I_{Gang}(x,y,t) - g^L V(x,y,t) + \eta_v(t)$$

  • \(V\) values above 1 set a refractory variable to a randomly drawn value
  • while the refractory value is larger than 0, \(V\) of that pixel is set to 0 and the refractory variable is decremented

References

[Wohrer2009]Wohrer, A., & Kornprobst, P. (2009). Virtual Retina: a biological retina model and simulator, with contrast gain control. Journal of Computational Neuroscience, 26(2), 219-49. http://doi.org/10.1007/s10827-008-0108-4

convis.retina

This module provides the retina model.

class convis.retina.Retina(opl=True, bipolar=True, gang=True, spikes=True)[source]

A retinal ganglion cell model comparable to VirtualRetina [Wohrer200923].

[Wohrer200923]Wohrer, A., & Kornprobst, P. (2009). Virtual Retina: a biological retina model and simulator, with contrast gain control. Journal of Computational Neuroscience, 26(2), 219-49. http://doi.org/10.1007/s10827-008-0108-4

See also

convis.base.Layer
The Layer base class, providing chunking and optimization
convis.filters.retina.OPL
The outer plexiform layer performs luminance to contrast conversion
convis.filters.retina.Bipolar
provides contrast gain control
convis.filters.retina.GanglionInput
provides a static non-linearity and a last spatial integration
convis.filters.retina.GanglionSpiking
creates spikes from an input current

Examples

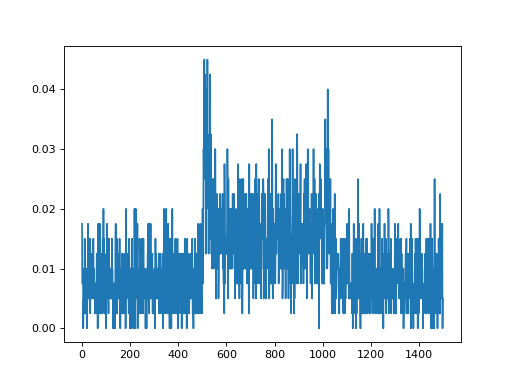
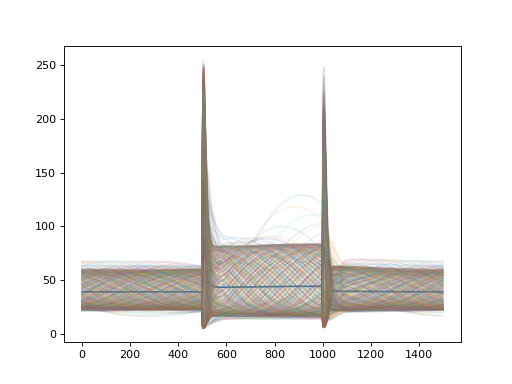
import convis
import numpy as np
from matplotlib import pylab as plt
retina = convis.retina.Retina()
inp = convis.samples.moving_grating(2000)
inp = np.concatenate([inp[:1000],2.0*inp[1000:1500],inp[1500:2000]],axis=0)
o_init = retina.run(inp[:500],dt=200)
o = retina.run(inp[500:],dt=200)
convis.plot_5d_time(o[0],mean=(3,4)) # plots the mean activity over time
plt.figure()
retina = convis.retina.Retina(opl=True,bipolar=False,gang=True,spikes=False)
o_init = retina.run(inp[:500],dt=200)
o = retina.run(inp[500:],dt=200)
convis.plot_5d_time(o[0],mean=(3,4)) # plots the mean activity over time
convis.plot_5d_time(o[0],alpha=0.1) # plots a line for each pixel

(Source code)

Attributes

opl (Layer (convis.filters.retina.OPL))
bipolar (Layer (convis.filters.retina.Bipolar))
gang_0_input (Layer (convis.filters.retina.GanglionInput))
gang_0_spikes (Layer (convis.filters.retina.GanglionSpiking))
gang_1_input (Layer (convis.filters.retina.GanglionInput))
gang_1_spikes (Layer (convis.filters.retina.GanglionSpiking))
_timing (list of tuples) timing information of the last run (last chunk) Each entry is a tuple of (function that was executed, number of seconds it took to execute)
keep_timing_info (bool) whether to store all timing information in a list
timing_info (list) stores timing information of all runs if keep_timing_info is True.

convis.filters.retina

class convis.filters.retina.SeperatableOPLFilter[source]

A fullly convolutional OPL implementation.

All filters are implemented as convolutions which makes this layer a lot slower than HalfRecursiveOPLFilter.

The following virtual parameters set the corresponding tensors with convolution filters. Eg. they turn the standard deviation of the gaussian into a numerical, circular gaussian.

You can set them to a value via .set(value) which will trigger them to re-calculate the filters.

See also

convis.retina.Retina, OPL, HalfRecursiveOPLFilter, FullConvolutionOPLFilter

Attributes

sigma_center (virtual parameter) Size of the center receptive field
tau_center (virtual parameter) Time constant of the center receptive field
n_center (virtual parameter) number of cascading exponential filters
undershoot_tau_center (virtual parameter) time constant of the high pass filter
undershoot_relative_weight_center (virtual parameter) relative weight of the high pass filter
sigma_surround (virtual parameter) Size of the surround receptive field
tau_surround (virtual parameter) Time constant of the surround receptive field
relative_weight (virtual parameter) relative weight between center and surround
center_G Spatial convolution filter for the center receptive field
center_E recursive temporal filter for the center receptive field
surround_G Spatial convolution filter for the surround receptive field
surround_E recursive temporal filter for the surround receptive field
class convis.filters.retina.HalfRecursiveOPLFilter[source]

The default OPL implementation.

Temporal filters are implemented recursively and spatial filters are convolution filters.

The following virtual parameters set the corresponding tensors with convolution filters. Eg. they turn the standard deviation of the gaussian into a numerical, circular gaussian.

You can set them to a value via .set(value) which will trigger them to re-calculate the filters.

See also

convis.retina.Retina, OPL, SeperatableOPLFilter, FullConvolutionOPLFilter

Attributes

sigma_center (virtual parameter) Size of the center receptive field
tau_center (virtual parameter) Time constant of the center receptive field
n_center (virtual parameter) number of cascading exponential filters
undershoot_tau_center (virtual parameter) time constant of the high pass filter
undershoot_relative_weight_center (virtual parameter) relative weight of the high pass filter
sigma_surround (virtual parameter) Size of the surround receptive field
tau_surround (virtual parameter) Time constant of the surround receptive field
relative_weight (virtual parameter) relative weight between center and surround
center_G (Conv3d) Spatial convolution filter for the center receptive field
center_E (Recursive Filter) recursive temporal filter for the center receptive field
surround_G (Conv3d) Spatial convolution filter for the surround receptive field
surround_E (Recursive Filter) recursive temporal filter for the surround receptive field
class convis.filters.retina.RecursiveOPLFilter[source]

The most efficient OPL implementation.

Temporal and spatial filters are implemented recursively.

The following virtual parameters set the corresponding tensors with convolution filters. Eg. they turn the standard deviation of the gaussian into a numerical, circular gaussian.

You can set them to a value via .set(value) which will trigger them to re-calculate the filters.

See also

convis.retina.Retina, OPL, SeperatableOPLFilter, FullConvolutionOPLFilter

Attributes

sigma_center (virtual parameter) Size of the center receptive field
tau_center (virtual parameter) Time constant of the center receptive field
n_center (virtual parameter) number of cascading exponential filters
undershoot_tau_center (virtual parameter) time constant of the high pass filter
undershoot_relative_weight_center (virtual parameter) relative weight of the high pass filter
sigma_surround (virtual parameter) Size of the surround receptive field
tau_surround (virtual parameter) Time constant of the surround receptive field
relative_weight (virtual parameter) relative weight between center and surround
center_G (Conv3d) Spatial convolution filter for the center receptive field
center_E (Recursive Filter) recursive temporal filter for the center receptive field
surround_G (Conv3d) Spatial convolution filter for the surround receptive field
surround_E (Recursive Filter) recursive temporal filter for the surround receptive field
class convis.filters.retina.FullConvolutionOPLFilter(shp=(100, 10, 10))[source]

Convolution OPL Filter

The VirtualParameters of the model create a 3d convolution filter. Any time they are changed, the current filter will be replaced! The VirtualParameters can not be optimized, only the convolution filter will change when using an optimizer.

See also

convis.retina.Retina, OPL, HalfRecursiveOPLFilter, SeperatableOPLFilter

class convis.filters.retina.OPL(**kwargs)[source]

The OPL current is a filtered version of the luminance input with spatial and temporal kernels.

$$I_{OLP}(x,y,t) = lambda_{OPL}(C(x,y,t) - w_{OPL} S(x,y,t)_)$$

with:

\(C(x,y,t) = G * T(wu,Tu) * E(n,t) * L (x,y,t)\)

\(S(x,y,t) = G * E * C(x,y,t)\)

In the case of leaky heat equation:

\(C(x,y,t) = T(wu,Tu) * K(sigma_C,Tau_C) * L (x,y,t)\)

\(S(x,y,t) = K(sigma_S,Tau_S) * C(x,y,t)\) p.275

This Layer can use one of multiple implementations. HalfRecursiveOPLFilter and SeperatableOPLFilter both accept the same configuration attributes. Or FullConvolutionOPLFilter which does not accept the parameters, but offers a single, non-separable convolution filter.

See also

convis.retina.Retina, HalfRecursiveOPLFilter, SeperatableOPLFilter, FullConvolutionOPLFilter

Attributes

opl_filter (Layer) The OPL filter that is used. Either HalfRecursiveOPLFilter, SeperatableOPLFilter or FullConvolutionOPLFilter.
class convis.filters.retina.Bipolar(**kwargs)[source]

Example Configuration:

'contrast-gain-control': {
    'opl-amplification__Hz': 50, # for linear OPL: ampOPL = relative_ampOPL / fatherRetina->input_luminosity_range ;
                                               # `ampInputCurrent` in virtual retina
    'bipolar-inert-leaks__Hz': 50,             # `gLeak` in virtual retina
    'adaptation-sigma__deg': 0.2,              # `sigmaSurround` in virtual retina
    'adaptation-tau__sec': 0.005,              # `tauSurround` in virtual retina
    'adaptation-feedback-amplification__Hz': 0 # `ampFeedback` in virtual retina
},

See also

convis.retina.Retina

Attributes

opl-amplification__Hz
  1. for linear OPL: ampOPL = relative_ampOPL / fatherRetina->input_luminosity_range ; ampInputCurrent in virtual retina bipolar-inert-leaks__Hz: 50 gLeak in virtual retina adaptation-sigma__deg: 0.2 sigmaSurround in virtual retina adaptation-tau__sec: 0.005 tauSurround in virtual retina adaptation-feedback-amplification__Hz: 0 ampFeedback in virtual retina
class convis.filters.retina.GanglionInput(**kwargs)[source]

The input current to the ganglion cells is filtered through a gain function.

\(I_{Gang}(x,y,t) = G * N(eT * V_{Bip})\)

\(N(V) = \frac{i^0_G}{1-\lambda(V-v^0_G)/i^0_G}\) (if \(V < v^0_G\))

\(N(V) = i^0_G + \lambda(V-v^0_G)\) (if \(V > v^0_G\))

Example configuration:

{
    'name': 'Parvocellular Off',
    'enabled': True,
    'sign': -1,
    'transient-tau__sec':0.02,
    'transient-relative-weight':0.7,
    'bipolar-linear-threshold':0,
    'value-at-linear-threshold__Hz':37,
    'bipolar-amplification__Hz':100,
    'sigma-pool__deg': 0.0,
    'spiking-channel': {
        ...
    }
},
{
    'name': 'Magnocellular On',
    'enabled': False,
    'sign': 1,
    'transient-tau__sec':0.03,
    'transient-relative-weight':1.0,
    'bipolar-linear-threshold':0,
    'value-at-linear-threshold__Hz':80,
    'bipolar-amplification__Hz':400,
    'sigma-pool__deg': 0.1,
    'spiking-channel': {
        ...
    }
},

See also

convis.retina.Retina, GanglionSpiking

Examples

Setting the virtual Parameters:

>>> m = convis.filters.retina.GanglionInput()
>>> m.sigma_surround.set(0.1)

Attributes

i_0 (Parameter)
v_0 (Parameter)
lambda_G (Parameter)
spatial_pooling (Conv3d) convolution Op for spatial pooling. Can be set to a gaussian with sigma_surround.set()
sigma_surround (VirtualParameter) sets spatial_pooling to be a gaussian of a certain standard deviation
transient convolution Op for high pass filtering
class convis.filters.retina.GanglionSpiking(**kwargs)[source]

The ganglion cells recieve the gain controlled input and produce spikes.

When the cell is not refractory, \(V\) moves as:

$$ \dfrac{ dV_n }{dt} = I_{Gang}(x_n,y_n,t) - g^L V_n(t) + eta_v(t)$$

Otherwise it is set to 0.

See also

convis.retina.Retina, GanglionInput

Attributes

refr_mu (Parameter) The mean of the distribution of random refractory times (in seconds).
refr_sigma (Parameter) The standard deviation of the refractory time that is randomly drawn around refr_mu
noise_sigma (Parameter) Amount of noise added to the membrane potential.
g_L (Parameter) Leak current (in Hz or dimensionless firing rate).

convis.retina_virtualretina

This module provides compatibility and default configurations for the convis retina model and the VirtualRetina software package.

This module is a compatibility layer between the Virtual Retina configurations and behaviour and the python implementation.

class convis.retina_virtualretina.RetinaConfiguration(updates={})[source]

A configuration object that writes an xml file for VirtualRetina.

(When this is altered, silver.glue.RetinaConfiguration has to also be updated by hand)

Does not currently care to parse an xml file, but can save/load in json instead. The defaults are equal to human.parvo.xml.

Values can be changed either directly in the configuration dictionary, or with the set helperfunction:

config = silver.glue.RetinaConfiguration()
config.retina_config['retina']['input-luminosity-range'] = 200
config.set('basic-microsaccade-generator.enabled') = True
config.set('ganglion-layers.*.spiking-channel.sigma-V') = 0.5 # for all layers
get(key, default=None)[source]

Retrieves values from the configuration.

conf.set(“ganglion-layers.*.spiking-channel.sigma-V”,None) # gets the value for all layers conf.set(“ganglion-layers.0”,{}) # gets the first layer

set(key, value, layer_filter=None)[source]

shortcuts for frequent configuration values

Knows where to put:

‘pixels-per-degree’, ‘size__deg’ (if x and y are equal), ‘uniform-density__inv-deg’ all attributes of linear-version all attributes of undershoot

Understands dot notation:

conf = silver.glue.RetinaConfiguration()
conf.set("ganglion-layers.2.enabled",True)
conf.set("ganglion-layers.*.spiking-channel.sigma-V",0.101) # changes the value for all layers

But whole sub-tree dicitonaries can be set as well (they replace, not update):

conf.set('contrast-gain-control', {'opl-amplification__Hz': 50,
                                    'bipolar-inert-leaks__Hz': 50,
                                    'adaptation-sigma__deg': 0.2,
                                    'adaptation-tau__sec': 0.005,
                                    'adaptation-feedback-amplification__Hz': 0
                                })

New dictionary keys are created automatically, new list elements can be created like this:

conf.set("ganglion-layers.=.enabled",True) # copies all values from the last element
conf.set("ganglion-layers.=1.enabled",True) # copies all values from list element 1
conf.set("ganglion-layers.+.enabled",True) # creates a new (empty) dictionary which is probably underspecified

conf.set("ganglion-layers.+",{
            'name': 'Parvocellular On',
            'enabled': True,
            'sign': 1,
            'transient-tau__sec':0.02,
            'transient-relative-weight':0.7,
            'bipolar-linear-threshold':0,
            'value-at-linear-threshold__Hz':37,
            'bipolar-amplification__Hz':100,
            'spiking-channel': {
                'g-leak__Hz': 50,
                'sigma-V': 0.1,
                'refr-mean__sec': 0.003,
                'refr-stdev__sec': 0,
                'random-init': 0,
                'square-array': {
                    'size-x__deg': 4,
                    'size-y__deg': 4,
                    'uniform-density__inv-deg': 20
                }
            }
        }) # ganglion cell layer creates a new dicitonary
read_json(filename)[source]

Reads a full retina config json file.

write_json(filename)[source]

Writes a retina config json file.

write_xml(filename)[source]

Writes a full retina config xml file.

Attributes that are not understood by the original Virtual Retina are removed.

convis.retina_virtualretina.deriche_filter_density_map(retina, sigma0=1.0, Nx=None, Ny=None)[source]

Returns a map of how strongly a point is to be blurred.

Relevant config options of retina:

'log-polar-scheme' : {
    'enabled': True,
    'fovea-radius__deg': 1.0,
    'scaling-factor-outside-fovea__inv-deg': 1.0
}

or for a circular (constant) scheme:

'log-polar-scheme' : {
    'enabled': False,
    'fovea-radius__deg': 1.0,
    'scaling-factor-outside-fovea__inv-deg': 1.0
}

The output should be used with retina_base.deriche_coefficients to generate the coefficient maps for a Deriche filter.